小学的时候学过分数的通分，比如像这种分母是二，分母是三，因为二和三两个的公倍数是六，所以就可以把二分之一写成六分之三。

六分之三是怎么来的？是分母乘以三，意味着分子同样乘以三，所以就变成了六分之三。三分之一如果想要分母变成六，相当于在分母上乘以了二，意味着分子也需要乘以二，所以三分之一可以写成六分之二。

现在三分之一和二分之一这两个分数就通分完成，把分母写成了相同的数字六，这个过程叫做分数的通分。以此类推，六分之一和三分之一进行通分。因为六是三的倍数，所以可以直接把三分之一写成六分之二。

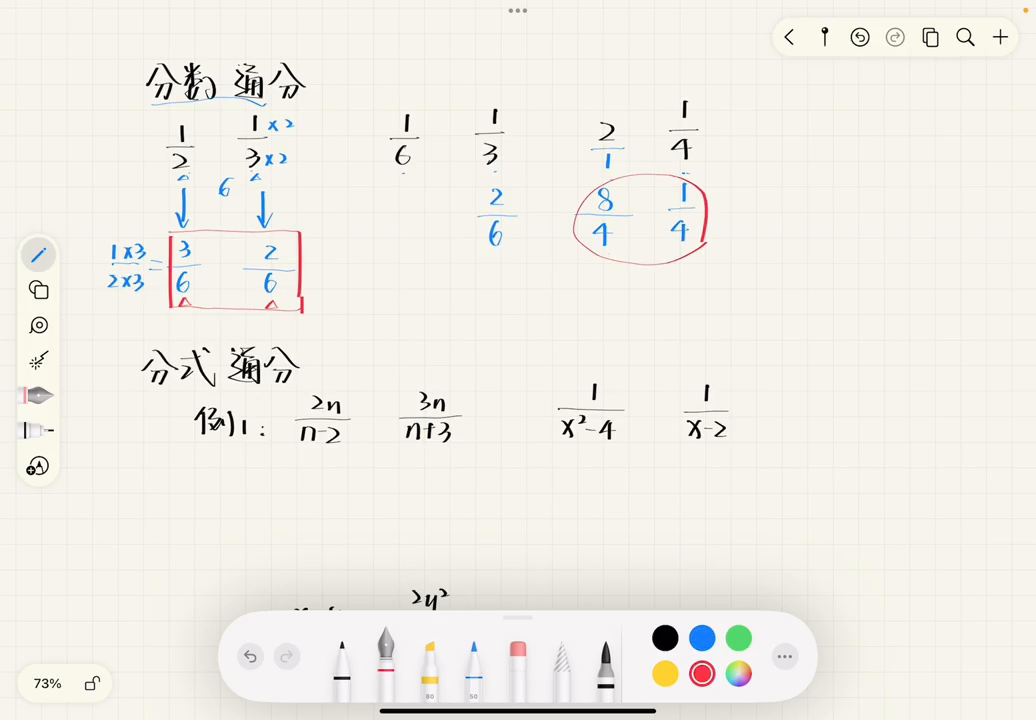
再来看二和四分之一，二是一个整数，对于整数进行通分时通常会把它看成是一个一分之几的分数，例如二就可以看成是一分之二，所以一和四的公倍数是四，就可以把分母一变成四，也就是乘以了四，所以分子二也要跟着乘以四变成八。

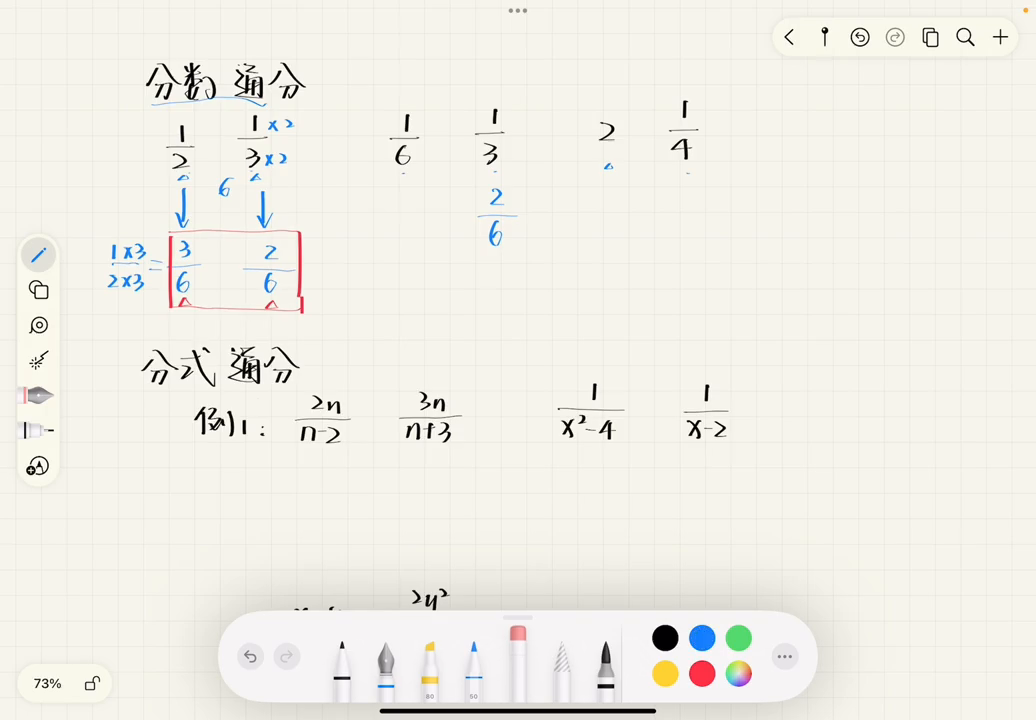
现在就通分完成，把二和四分之一通分成了分母是四的两个分数。分式的通分和分数的通分其实是非常类似的。

来看这个题目，第一个题目n减二和n加三是完全不一样的两个式子，因此首先找到两个的公分母，也就是n减二乘以n加三，其实相比数字更好找到公分母，通常就是拿两个相乘。

第一个式子n减二分之二n，如果想把分母写成n减二乘以n加三，意味着分母乘以了n加三，分子也同样去乘以n加三就可以了，所以第一个式子同分完成。

第二个式子如果想把分母写成n减二乘以n加三，分子也是一样的去乘以n减二，因为分母乘以n减二，所以分子也就乘以n减二。现在这两个式子就通分完成，它们的分母变成一样的n减二乘以n加三。

总结一下分式进行通分的步骤。

·第一步，先找公分母。

·第二步，找到公分母之后分母和分子要同乘或者同时扩大或缩小。

其实就是这两个步骤。

接着再来看下一个，比如第二个例题，看到两个分母是不一样的，但是n x的平方减四很明显是可以进行因式分解的，也就是要学会进行通分，需要有因式分解的知识储备。x平方减四可以因式分解为x减二乘以x加二，跟第二个式子x减二分之一可以发现前面的式子是后面式子的倍数的关系，所以公分母就可以确定为是x减二乘以x加二。

·确定好之后只需要把第二个式子进行运行，分母原本是x减2，现在分母乘上了一个x加2，意味着分子也需要乘以x加2，原本的分子是1乘以任何式子，还是这个数字，所以通分完之后就是x减2，长x加2分之x加2。现在它们两个分布一致就通分完成了。

·最后一个式子，这是一个整式，这是一个分式，这和在前面说过的分数的通分方法是一样的。先把这个整式看成是一个1分之x减y，然后再去找一下1和x加y的公分母，它们两个公分母就是x加y。

所以第一个式子的分母如果想要变成x加y，其实也就是拿原本的1乘以了一个x加y，意味着它的分子也需要乘一个x加y，分子就变成了x减y乘以x加y，一个式子就推荐完成。第二式子分母直接就是一个x加y，所以现在它们两个分母一致意味着已经配合完成了。

这就是分式的通分。