什么是方程的增根和无解(分式方程-无解)
2024-09-28 10:46:07 家电
关于x的分式方程,分母为0时x的值叫做方程的增根.
有时候,还会出现分式方程无解时,求方程中其它字母值的问题.
增根与无解的关系是:
(1)分式方程取增根时,分式方程一定无解;
(2)分式方程无解,除了未知数取增根外,还有一种情况,就是把分式方程转化为整式方程后,找不到未知数的值满足方程.
简单地说:增根只看x(设方程是关于x的方程),无解看所有未知数。
例 当m=________时,分式方程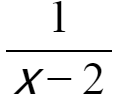 =
=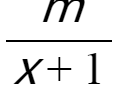 无解.
无解.
解析
(1) 分式方程转化为整式方程,这个方程含有两个未知数x、m.
(2) 由增根求出x的值,再把x的值代入整式方程,即可求出m的值.
(3) 把关于x的项合并,再假设系数为0,求得m的值。
(4) 原方程去分母,得:x+1=m(x-2),即(m-1)x-2m-1=0.
①若方程有增根,则x-2=0,或x+1=0,
∴x=2,或x=-1,
x=2时无m值;x=-1时m=0.
②设m-1=0,则方程(m-1)x-2m-1=0中不存在x,则表示原方程无解.此时,m=1.
(5) 关于x的方程,如果不存在x的项,则表示方程无解.为了使x不存在,可以在分式方程化为整式方程后合并x的项,再假设系数为0即可.
答案 0或1
练习
1. 如果分式方程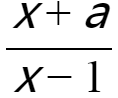 =a无解,则a的值是__________.
=a无解,则a的值是__________.
2. 如果分式方程2m+ =0无解,则m的值是_______.
=0无解,则m的值是_______.

曲径通幽
1.
解析
(1) 原方程去分母,得:x+a=a(x-1),即(a-1)x-2a=0.
(2) 若方程有增根,则x-1=0,∴x=1,∴a=-1.
(3) 设a-1=0,则方程(a-1)x-2a=0中不存在x,此时a=1.
答案 -1或1
2.
解析
(1) 原方程去分母,得:2m(x-1)+m+x=0,即(2m+1)x-m=0.
(2) 若方程有增根,则x-1=0,∴x=1,此时m=-1.
(3) 设2m+1=0,则方程(2m+1)x-m=0中不存在x,此时,m=-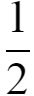 .
.
答案 -1或-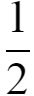
猜你喜欢

今日辟谣(2025年9月15日)

Ciiq保险柜用户售后服务中心实时反馈-今-日-更-新(Ciiq保险柜险柜密码怎么设置密码)

美的保险柜24小时人工售后服务为客户解决常见故障分析与处理(美的保险柜机械保险柜密码忘了怎么办)

卡植欧保险柜售后服务热线及保养指南(卡植欧保险柜保险柜打不开怎么弄)

沸福保险柜用户售后服务中心实时反馈-今-日-汇-总(沸福保险柜保险柜怎么打开)

龙觇保险柜售后服务24小时服务热线-全国400服务号码实时反馈-今-日-汇-总(龙觇保险柜电子保险柜打不开怎么办)
今日辟谣(2025年9月15日)

Ciiq保险柜用户售后服务中心实时反馈-今-日-更-新(Ciiq保险柜险柜密码怎么设置密码)

美的保险柜24小时人工售后服务为客户解决常见故障分析与处理(美的保险柜机械保险柜密码忘了怎么办)

卡植欧保险柜售后服务热线及保养指南(卡植欧保险柜保险柜打不开怎么弄)

沸福保险柜用户售后服务中心实时反馈-今-日-汇-总(沸福保险柜保险柜怎么打开)

龙觇保险柜售后服务24小时服务热线-全国400服务号码实时反馈-今-日-汇-总(龙觇保险柜电子保险柜打不开怎么办)

丛林狐保险柜售后服务号码及其服务网点介绍实时反馈全+境+到+达(丛林狐保险柜迷你世界保险柜怎么用)

宝宸侠保险柜全国各市售后服务热线号码实时反馈-今-日-更-新(宝宸侠保险柜保险柜没电池怎么打开)

悦倪保险柜售后服务维修号码实时反馈全+境+到+达(悦倪保险柜保险柜怎么换电池图示)

耐辉顿保险柜全国统一服务热线-全国24小时服务中心实时反馈-今-日-资-讯(耐辉顿保险柜保险柜没电了怎么开锁)